In my first blog post i will show you my short journey into std::ranges. Ranges were introduced in the C++20 standard and originated from the rangeV3 library.
In especially, the iteration over collections are super simple now. They also allow to iterate over the results of some member function. This is called projection. I also discuss two example where other capabilities as filtering and views in general are shown

Example 1: Projection onto member functions

Consider the following struct which has three member functions:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
struct Shape
{
  double getArea()
  {
  return /*calc area */ ;
  }

  double getVolume()
  {
  return /*calc volume */ ;
  }

  std:pair<double,double> getVolumeAndArea()
  {
  return std::make_pair<double,double>(getVolume(), getArea());
  }

/* some data members */
}

Now we have a vector of shapes and want to iterate over the vector but we want as quantity directly the return value of the member function, i.e. we have

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int main(){

std:vector<Shape> shapes;
/* fill shapes */

for(const auto area : area(shapes))
  /* do something with area */


for(const auto volume : volume(shapes))
  /* do something with volume */


for(const auto [volume, area] : volumeAndArea(shapes))
  /* do something with volume and area */
}

This behavior can be accomplished with so called views in std::ranges. We need for this task std::ranges::views::transform or the synonym std::ranges::transform_view to which we can directly pass a pointer to a member function.

We can then write

1
2
for(const auto area : std::ranges::transform_view(shapes, &Shape::getArea ))
        std::cout << area << "\n";

which can also be wrapped obviously into a function

1
2
3
4
5
auto area(std::vector<Shape>& shapes)
{
    using std::ranges::transform_view;
    return transform_view(shapes, &Shape::getArea);
}

godbolt.org

transform_view is also suited for a more general approach. We can plugin anything invokable, e.g. lambdas as follows

1
2
3
4
5
int i = 0;
   auto lambda = [&i](auto& shape){return i++*shape.getArea(); };
   for(const auto areaMultiples :  std::ranges::transform_view(shapes, lambda ))
       std::cout << areaMultiples << "\n";

godbolt.org

I think this approach pretty nice since it reduces a lot of noise around how to iterate over collections.

Using the lambda we can also call member functions which need arguments.
If we have the member function as follows

1
2
3
4
5
6
7
8
struct Shape
{
  double getArea(int i)
  {
    return 42*i;
  }
};

We can also use it in the following way

1
2
3
4
int i = 0;
auto lambda = [&i](auto& shape){return shape.getArea(i++); };
for(const auto areaMultiples :  transform_view(shapes, lambda ))
    std::cout << areaMultiples << "\n";

godbolt.org

Example 2: Iterate over a filtered subset of a collection

Another nice example is the feature to filter automatically the stuff which you are not interested in.
This can be done with std::ranges::filter_view or again with the synonym std::ranges::views::filter.

We have a vector of integers. We only want to iterate over the prime numbers. This can be done in the following old school way:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
bool isPrime(int n)
{
    if (n <= 1)
        return false;

    for (int i = 2; i <= std::sqrt(n); i++)
        if (n % i == 0)
            return false;

    return true;
}

int main() {
  std::vector<int> v{0,1,2,3,4,5};

  for(int i : v)
        if(isPrime(i)) /* byhand label in the figure */
          /* do something with the primes */

}

Using the ranges library we can write

1
2
3
4
5
6
int main() {
  std::vector<int> v{0,1,2,3,4,5};

  for(int i :  std::ranges::filter_view(v,isPrime)) /* ranges2 label in the figure */
          /* do something with the primes */
}

or equivalently

1
2
3
4
5
6
int main() {
  std::vector<int> v{0,1,2,3,4,5};

  for(int i : v | std::views::filter(isPrime)) /* ranges1 label in the figure */
          /* do something with the primes */
}

where the operator | unites the predicate isPrime with the vector v.
I also benchmarked all three examples at quickbench using a vector with 1000 entries, see Figure below.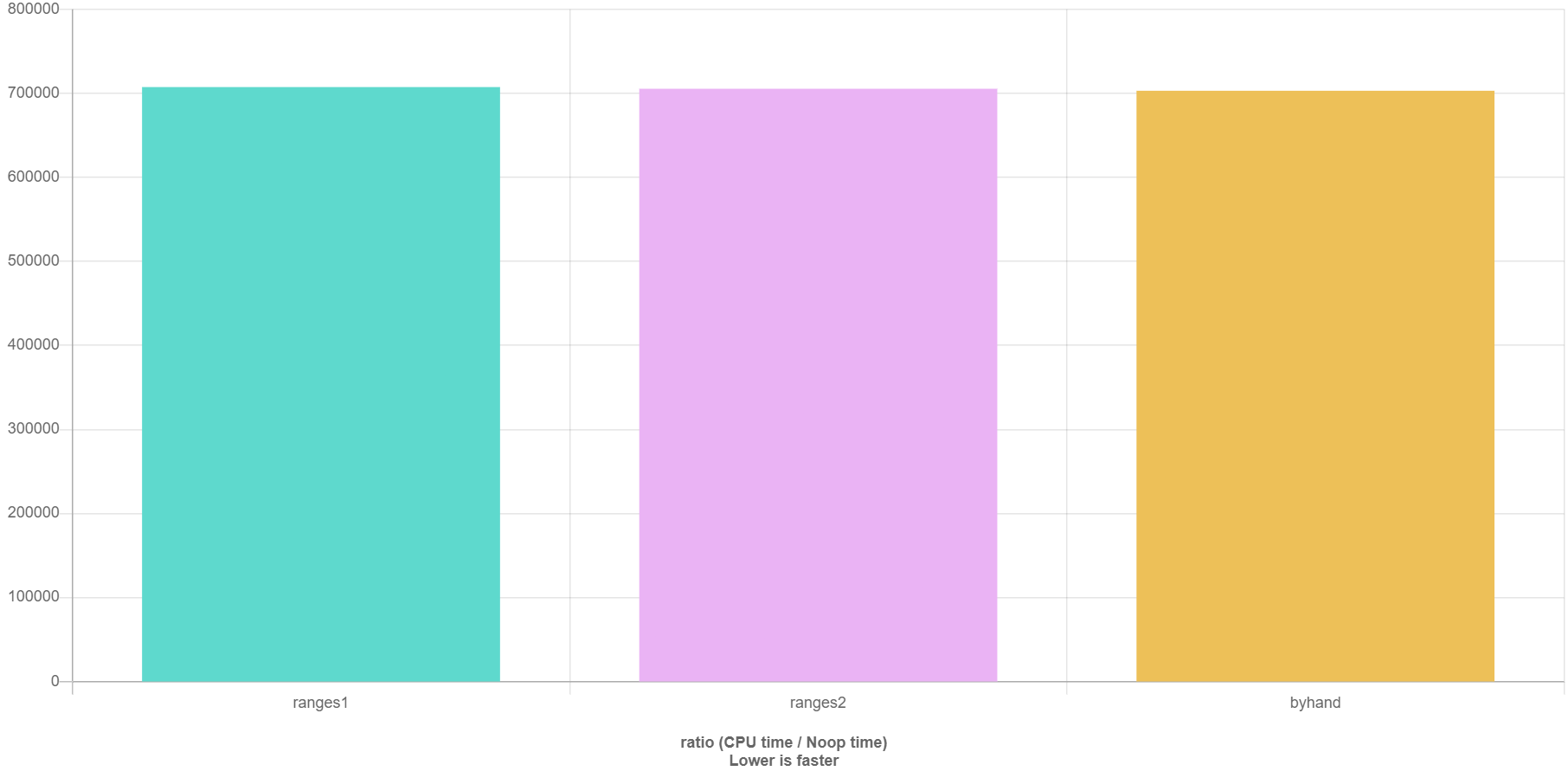

As you can see, there is almost no difference in the time taken. At least for the gcc10.2 compiler.

Nevertheless, if we change the predicate isPrime to something trivial, e.g.

1
bool isPrime(int n){    return true;}

The benchmark result changes to quickbench.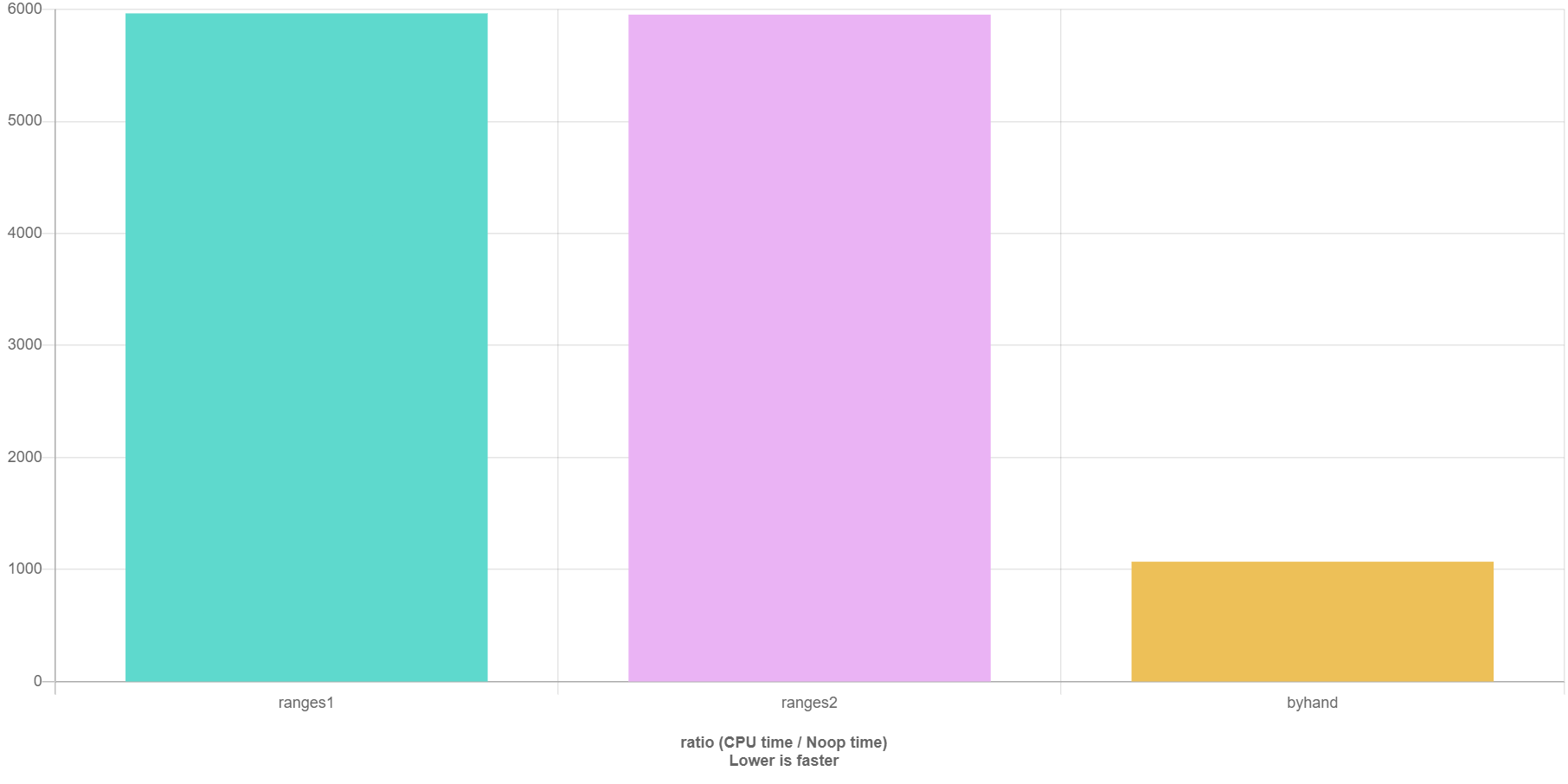

Here, one can see that the by hand approach is much faster. In my opinion this is due to the inlining of the function in the byHand approach.

Intrestingly, if i change the predicate slightly by introducing the function to be constexpr.

1
2
3
4
constexpr bool isPrime(int n)
{
    return true;
}

the results are again quite different and the ranges1 approach gains speed: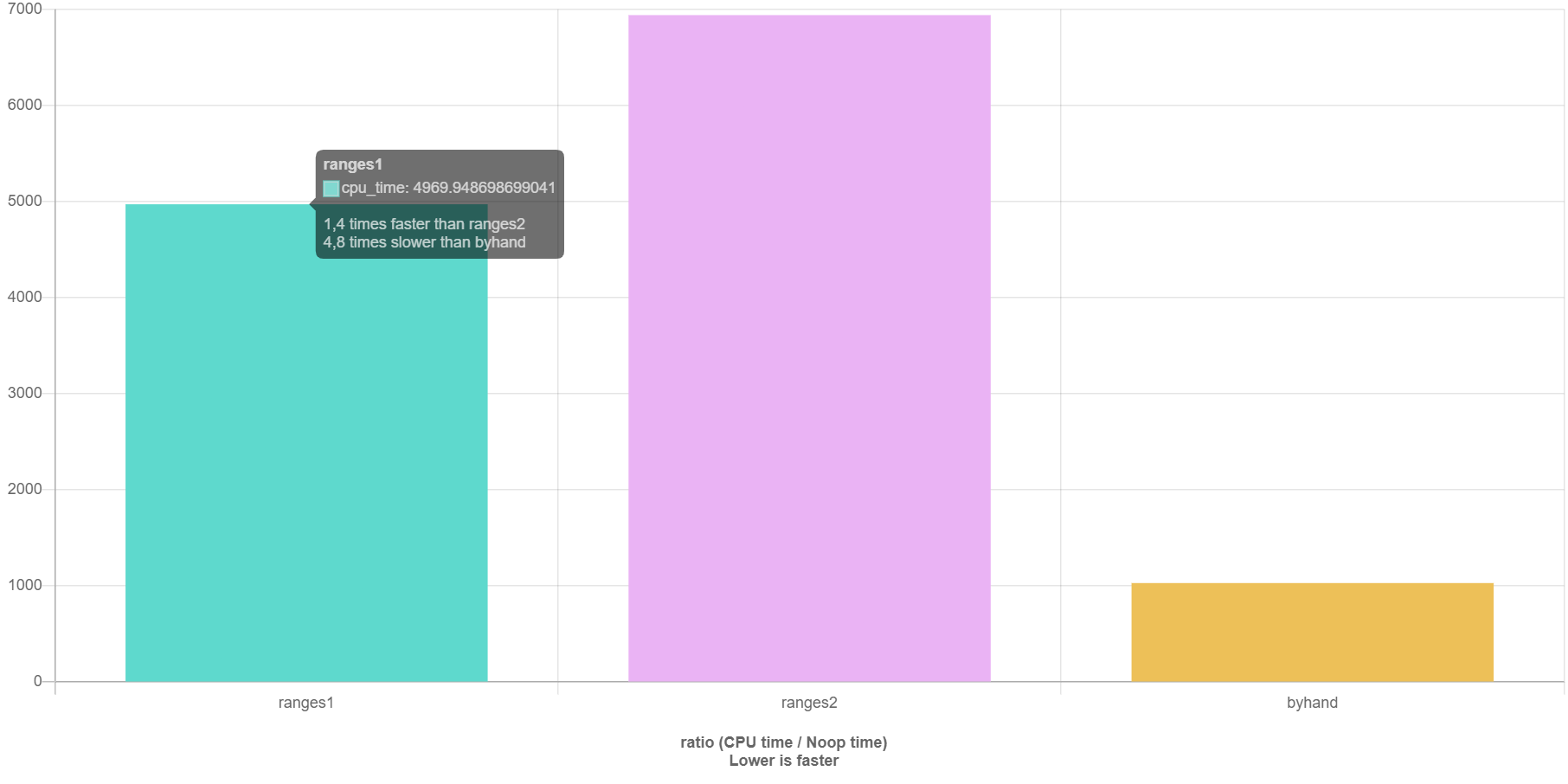

Example 3: Iterate over a view without storing any collection directly

In the example before i always wrote std::vector<int> v{0,1,2,3,4,5}; to define a vector over which we iterated. As you may have noticed, i used a different approach in the benchmark examples. With the ranges library you can construct views directly and never even have to store the complete vector. E.g. we can use std::ranges::iota_view as follows

1
2
3
auto v = std::ranges::iota_view{1, 1000};
 for (auto i : v)
  /* do something with i */

or directly

1
2
for (auto i : std::ranges::iota_view{1, 1000})
  /* do something with i */

Bonus: Chaining stuff together

You can also chain operation together, e.g. if we want to iterate over the square of primes:

1
2
3
4
5
6
int main() {
  std::vector<int> v{0,1,2,3,4,5};
   auto square = [](int i) { return i * i; };
  for(int i : v | std::views::filter(isPrime) | std::views::transform(square))
          /* do something with the squares of primes */
}

At least to me these views seem to be really powerful.